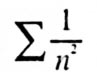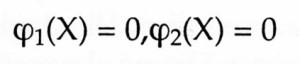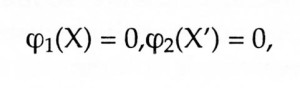Qualche anno fa ho avuto occasione di esporre alcune idee sulla logica dell’infinito, sull’impiego dell’infinito in Matematica, sull’uso che se ne fa da Cantor in poi; ho spiegato perché non ritenevo legittime certe modalità di ragionamento di cui avevano creduto potersi servire alcuni matematici eminenti. Mi tirai ovviamente addosso delle repliche violente; questi matematici erano convinti di non essersi sbagliati, credevano di avere avuto il diritto di fare quello che avevano fatto. La discussione andava per le lunghe, non che si vedessero continuamente comparire argomenti nuovi, ma per il fatto che si girava sempre nello stesso cerchio, ciascuno ripetendo quello che aveva appena detto senza far mostra di aver inteso quello che l’avversario aveva detto. Mi veniva in ogni momento spedita una nuova dimostrazione del principio contestato, per mettersi, così si diceva, al riparo da ogni obiezione; ma questa dimostrazione era sempre la stessa, con il trucco appena rifatto. Non si è quindi giunti a nessuna conclusione; se dicessi di esserne rimasto sorpreso darei un’idea triste della mia capacità di penetrazione psicologica.
In queste condizioni conviene ripetere una volta di più gli stessi argomenti, ai quali potrei forse dare una forma nuova, ma della sostanza dei quali non potrei cambiare niente, dal momento che mi pare non si sia neanche cercato di confutarli. Mi sembra preferibile cercare quale possa essere l’origine di una differenza di mentalità tale da generare queste divergenze nei punti di vista. Ho appena detto che queste divergenze irriducibili non mi avevano sorpreso, che le avevo previste fin dal primo momento, ma questo non ci dispensa dal cercarne una spiegazione; possiamo prevedere un fatto in seguito ad esperienze ripetute e trovarci tuttavia in forte imbarazzo a spiegarlo.
Cerchiamo dunque di studiare la psicologia delle due scuole rivali, da un punto di vista puramente oggettivo, come se noi stessi fossimo collocati al di fuori di queste scuole, come se descrivessimo una guerra tra due formicai; constateremo in prima battuta l’esistenza tra i matematici di due tendenze opposte nella maniera di considerare l’infinito. Per gli uni, l’infinito deriva dal finito, c’è un infinito in quanto c’è un’infinità di cose finite possibili; per gli altri l’infinito preesiste al finito, il finito si ottiene staccando un pezzettino nell’infinito.
Un teorema deve poter essere verificato ma, visto che noi stessi siamo finiti, non possiamo operare che su oggetti finiti; anche ammettendo quindi che la nozione di infinito abbia un ruolo nell’enunciato del teorema, occorre che nella verifica non se ne faccia più menzione; altrimenti la verifica sarebbe impossibile.
Porterò come esempi teoremi di questo genere: la successione dei numeri interi è illimitata, la serie
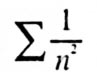
è convergente, ecc.; ciascuno di essi può tradursi in uguaglianze o disuguaglianze in cui non figurino che numeri finiti. Questi teoremi partecipano dell’infinito, non in quanto una delle verifiche possibili ne partecipi essa stessa, ma in quanto le verifiche possibili sono in numero infinito.
Enunciando il teorema affermo che tutte queste verifiche avranno successo; ben inteso, non le si fanno tutte; ce ne sono di quelle che chiamo possibili perché non esigerebbero che un tempo finito, ma che sarebbero impossibili in pratica perché richiederebbero anni di lavoro. Mi basta che si possa concepire qualcuno abbastanza ricco ed abbastanza pazzo da tentare l’impresa pagando un numero sufficiente di aiutanti. La dimostrazione del teorema ha come scopo esattamente quello di rendere inutile questa follia.
Ha senso un teorema che non comporti alcuna conclusione verificabile? o, più in generale, un teorema qualsiasi ha senso al di fuori delle verifiche che comporta? È su questo punto che i matematici si dividono. Quelli della prima scuola, quelli che chiamerò Pragmatisti (dato che bisogna pur dare loro un nome) rispondono di no, e quando viene presentato loro un teorema senza fornire un mezzo per verificarlo non ci vedono che acqua fresca. Costoro non vogliono prendere in considerazione che oggetti che possano essere definiti in un numero finito di parole; quando nel corso di un ragionamento parliamo loro di un oggetto A che soddisfa a certe condizioni, essi sottintendono un oggetto che soddisfa a queste condizioni quali che siano le parole di cui ci si servirà per definirlo, purché queste parole siano in numero finito.
Quelli dell’altra scuola, che chiamerò per brevità Cantoriani, non sono disposti ad ammettere tutto ciò; un uomo, per quanto sia chiacchierone, non pronuncerà mai nella sua vita più di un miliardo di parole; vogliamo dunque escludere dalla Scienza gli oggetti la cui definizione richieda un miliardo di parole più una? e se non li escludiamo, perché dovremmo escludere quelli che non possono essere definiti che con un’infinità di parole, dal momento che la costruzione degli uni come quella degli altri è al di fuori della portata dell’umanità?
Quest’argomento lascia ovviamente freddi i Pragmatisti; per quanto chiacchierone sia un uomo, l’umanità sarà ancora più chiacchierona e, visto che non sappiamo quanto tempo durerà, non possiamo limitare in anticipo il dominio delle sue investigazioni; sappiamo soltanto che questo dominio resterà sempre limitato; ed anche se potessimo fissare la data della sua scomparsa ci sarebbero altri che potrebbero riprendere l’opera lasciata incompiuta sulla Terra; i Pragmatisti non avrebbero d’altronde alcuna remora ad immaginare un’umanità molto più chiacchierona della nostra, ma che conservi ancora qualcosa di umano; essi si rifiutano di ragionare sull’ipotesi di non so quale divinità infinitamente chiacchierona e capace di pensare un’infinità di parole in un tempo finito. E gli altri pensano al contrario che gli oggetti esistano, in una sorta di grande negozio, indipendentemente da qualsiasi umanità o divinità che potesse parlarne o pensarci; che in questo negozio possiamo fare la nostra scelta, che molto probabilmente non abbiamo abbastanza appetito o abbastanza denaro per comprare tutto; ma che l’inventario del negozio sia indipendente dalle risorse degli acquirenti. E da questo malinteso iniziale discende ogni genere di divergenza sulle questioni di dettaglio.
Prendiamo ad esempio il teorema di Zermelo, secondo il quale lo spazio può essere trasformato in un insieme ben ordinato; i Cantoriani saranno sedotti dal rigore, reale o apparente, della dimostrazione; i Pragmatisti gli risponderanno: Dite di essere in grado di trasformare lo spazio in un insieme ben ordinato; ebbene! trasformatelo. – Sarebbe troppo lungo. – Allora mostrateci almeno che qualcuno che avesse abbastanza tempo e pazienza potrebbe compiere la trasformazione. – No, non lo possiamo perché il numero di operazioni da fare è infinito, è addirittura più grande di Aleph-con-zero. – Potete mostrare come si potrebbe esprimere in un numero finito di parole la legge che permetterebbe di ordinare lo spazio? – No. – Ed i Pragmatisti concludono che il teorema è privo di senso, o falso, o per lo meno non dimostrato.
I Pragmatisti si pongono dal punto di vista dell’estensione ed i Cantoriani dal punto di vista della comprensione. Quando si tratta di una collezione finita, questa distinzione non può interessare che i teorici della logica formale; ma essa ci appare molto più profonda nel caso delle collezioni infinite. Se ci si pone dal punto di vista dell’estensione una collezione si costituisce per aggiunta successiva di nuovi membri; possiamo, combinando i vecchi oggetti, costruire oggetti nuovi, con questi ultimi oggetti ancora più nuovi, e se la collezione è infinita è perché non c’è ragione di fermarsi.
Dal punto di vista della comprensione, al contrario, partiamo dalla collezione in cui si trovano oggetti preesistenti, che ci appaiono in un primo momento come indistinti, ma finiamo per riconoscere qualcuno di essi perché attacchiamo loro delle etichette e li sistemiamo in cassetti; ma gli oggetti sono anteriori alle etichette, e la collezione esisterebbe anche se non esistesse nessun catalogatore che la classificasse.
Per i Cantoriani la nozione di numero cardinale non comporta alcun mistero. Due collezioni hanno lo stesso numero cardinale quando le si può sistemare negli stessi cassetti; niente di più facile dal momento che le due collezioni preesistono, e che possiamo allo stesso modo considerare come preesistente una collezione di cassetti indipendente dai catalogatori incaricati di sistemarvi gli oggetti. Per i Pragmatisti le cose non vanno in questo modo; la collezione non è preesistente, ma s’arricchisce ogni giorno: si aggiungono continuamente nuovi oggetti, che non avremmo potuto definire senza appoggiarci alla nozione degli oggetti già classificati in precedenza ed alla maniera in cui sono stati classificati. Ad ogni nuova acquisizione il catalogatore può essere costretto a rivoluzionare i cassetti per trovare il modo di incasellarla: non sapremo mai se due collezioni possano sistemarsi negli stessi cassetti, dal momento che possiamo sempre temere che sia necessario rimetterli in ordine. Per esempio, i Pragmatisti non ammettono che oggetti che possano essere definiti in un numero finito di parole; le definizioni possibili, essendo esprimibili per mezzo di frasi, possono sempre essere numerate con numeri ordinari da uno fino all’infinito. In questo rispetto non ci sarebbe che un solo numero cardinale infinito possibile, il numero Aleph-con-zero; perché diciamo allora che la potenza del continuo non è quella dei numeri interi? Sì, dati tutti i punti dello spazio che sappiamo definire con un numero finito di parole, sappiamo immaginare una legge, esprimibile essa stessa con un numero finito di parole, che li faccia corrispondere alla successione dei numeri interi; ma consideriamo ora delle frasi in cui figuri la nozione di questa legge di corrispondenza; fino ad un attimo fa esse non avevano alcun senso, in quanto questa legge non era stata ancora inventata, e non potevano servire a definire punti dello spazio; ora hanno acquistato un senso, e ci permetteranno di definire nuovi punti dello spazio; ma questi nuovi punti non troveranno più posto nella classificazione adottata, il che ci costringerà a rivoluzionarla. Ed è questo quello che vogliamo dire quando diciamo, seguendo i Pragmatisti, che la potenza del continuo non è quella dei numeri interi. Vogliamo dire che è impossibile stabilire tra questi due insiemi una legge di corrispondenza che sia al riparo da questo genere di rivoluzione; mentre lo si può fare per esempio quando si tratta di una retta o di un piano. Quindi i Pragmatisti non sono certi che un insieme qualunque abbia, parlando in termini propri, un numero cardinale; oppure che dati due insiemi si possa sempre sapere se hanno la stessa potenza, o se uno ha una potenza più grande dell’altro. Arrivano così a dubitare dell’esistenza di Aleph-con-uno.
Un’altra fonte di divergenza viene dal modo di concepire la definizione. Ci sono più generi di definizione; le definizione diretta che può farsi sia per genus proximum et differentiam specificam sia per costruzione. Osserviamo di sfuggita che si danno definizioni incomplete, nel senso che definiscono non un individuo, ma un intero genere; esse sono legittime e sono anche quelle di cui si fa uso con maggiore frequenza; ma secondo i Pragmatisti occorre sottintendere l’insieme degli individui che soddisfano alla definizione e che potremmo definire completamente in un numero finito di parole; per i Cantoriani questa restrizione è artificiale e priva di significato.
Se non ci fossero che definizioni dirette l’impotenza della logica pura non potrebbe essere contestata; potremmo allora rimpiazzare ciascun termine di una qualunque proposizione con la sua definizione; portata a termine questa sostituzione la proposizione o non si ridurrebbe ad un’identità e non sarebbe quindi suscettibile di una dimostrazione puramente logica; oppure si ridurrebbe ad un’identità ed allora non sarebbe che una tautologia più o meno abilmente camuffata.
Ma abbiamo ancora un altro genere di definizioni, le definizioni per mezzo di postulati; in generale sapremo che l’oggetto da definire appartiene ad un genere, ma quando si tratterà di enunciare le differenze specifiche queste non verranno enunciate direttamente, ma con l’aiuto di un “postulato” cui l’oggetto definito dovrà soddisfare. È così che i matematici possono definire una quantità x per mezzo di un’equazione esplicita y = f(x) oppure per mezzo di un’equazione implicita F(x, y) = 0.
La definizione per mezzo di un postulato non ha valore se non quando si sia dimostrata l’esistenza dell’oggetto definito; in linguaggio matematico ciò vuoI dire che il postulato non implica contraddizione; non si ha il diritto di trascurare questa condizione; occorre o ammettere l’assenza di contraddizione come una verità intuitiva, come un assioma, per una sorta di atto di fede; ma allora occorre rendersi conto di quello che si fa e sapere che abbiamo allungato l’elenco degli assiomi indimostrabili; oppure occorre costruire una dimostrazione in piena regola, sia per mezzo dell’esempio, sia con l’impiego del ragionamento per ricorrenza. Non è che questa dimostrazione sia meno necessaria quando si tratta di una definizione diretta, ma è in generale più facile.
Certi Pragmatisti saranno più esigenti: per considerare legittima una definizione non basterà loro che non conduca a contraddizioni nei termini, pretenderanno anche che abbia un senso, secondo il loro punto di vista particolare che ho cercato di definire prima.
Sia come sia, la logica resterà sterile, dopo l’introduzione delle definizioni per mezzo di postulati? Non possiamo più, data una proposizione, rimpiazzare in essa un termine con la sua definizione; tutto quello che possiamo fare è eliminare questo termine tra la proposizione ed il postulato che gli serve di definizione. Se questa operazione, fatta secondo quelle che potremmo chiamare le regole dell’eliminazione logica, non ci conduce ad un’identità, la proposizione non è dimostrabile per mezzo della logica pura; se conduce ad un’identità, la proposizione non è che una tautologia. Non dovremo cambiare niente nelle nostre conclusioni di poco fa.
Ma esiste un terzo genere di definizioni, il che dà origine ad un nuovo malinteso tra Pragmatisti e Cantoriani. Sono ancora definizioni per mezzo di un postulato, ma il postulato è qui una relazione tra l’oggetto da definire e tutti gli individui di un genere cui lo stesso oggetto da definire è supposto fare parte (oppure di cui sono supposti fare parte enti che non possono essi stessi essere definiti che per mezzo dell’ oggetto da definire).
È quello che accade se poniamo i due postulati seguenti:
X (oggetto da definire) ha una certa relazione con tutti gli individui del genere G;
X fa parte del genere G;
oppure i tre postulati seguenti:
X ha una certa relazione con tutti gli individui del genere G;
Y ha una certa relazione con X;
Y fa parte di G.
Per i Pragmatisti, una definizione siffatta implica un circolo vizioso. Non si può definire X senza conoscere tutti gli individui del genere G, e di conseguenza senza conoscere X che è uno di questi individui. I Cantoriani non ammettono tutto ciò: il genere G ci è dato, di conseguenza ne conosciamo tutti gli individui, la definizione ha come scopo solo quello di discriminare tra questi individui quello che ha con tutti i suoi compagni la relazione enunciata. No, rispondono i loro avversari, la conoscenza del genere non vi fa conoscere tutti i suoi individui, vi dà solo la possibilità di costruirli tutti, o piuttosto di costruirne quanti ne vorrete. Non esisteranno che dopo che siano stati costruiti, cioè dopo che siano stati definiti; X non esiste che per mezzo della sua definizione, che non ha senso se non conosciamo in anticipo tutti gli individui di G ed in particolare X. Non servirebbe a niente dire, essi aggiungono, che definire X per mezzo della sua relazione con X non è un circolo vizioso, che questa relazione è in fin dei conti un postulato che può servire a definire X; perché occorrerebbe stabilire preliminarmente che questo postulato non implica contraddizione, ma non è questo che viene fatto di solito in questo genere di definizioni. Si dimostra in primo luogo che, quale che sia il genere G, di cui tutti gli individui sono supposti conosciuti, esiste un ente X che ha con questo genere la relazione in questione; cioè che l’esistenza di questo ente non implica contraddizione; resterebbe da far vedere che non c’è contraddizione tra l’esistenza di questo ente e l’ipotesi che questo stesso ente faccia parte del genere.
Il dibattito potrebbe andare per le lunghe; ma il punto che vorrei mettere in evidenza è che, se ammettessimo questo genere di definizioni, la logica non sarebbe più sterile, e prova ne è che è stata messa in piedi una pletora di ragionamenti destinati a dimostrare proposizioni che non erano assolutamente tautologie, dato che ci sono persone che si chiedono se non siano false. Non possiamo allora che ammirare il potere che può avere una parola. Ecco un oggetto da cui non si sarebbe potuto ricavare nulla, quando non era ancora stato battezzato; è stato sufficiente dargli un nome perché facesse meraviglie. Come è stato possibile tutto ciò? Il fatto è che dandogli un nome abbiamo affermato implicitamente che l’oggetto esisteva (era cioè scevro da ogni contraddizione) e che era completamente determinato. Ora, secondo i Pragmatisti di ciò non sappiamo niente. Qual è dunque il meccanismo che rende feconda la dimostrazione? Ma è proprio semplice, si nega la proposizione da dimostrare e si mostra che ci si trova in contraddizione con l’esistenza dell’oggetto X; e ciò è legittimo solo a condizione di essere certi di questa esistenza, e, d’altra parte, se sappiamo che l’oggetto è interamente determinato. Ed in effetti se X è dedotto dal genere G per mezzo della definizione, e se in seguito completiamo il genere G aggiungendogli l’oggetto X e gli altri individui dello stesso genere che possono derivarne; e chiamiamo G’ il genere così completato e X’ ciò che verrebbe dedotto da G’ per mezzo della definizione allo stesso modo in cui X è stato dedotto da G, occorre essere sicuri che X’ sia identico ad X. Se non fosse questo il caso e se, negando la proposizione da dimostrare, si fosse condotti a due enunciati contraddittori
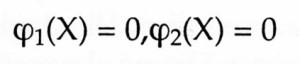
come potremmo sapere che è proprio lo stesso X che figura nell’uno e nell’altro? Se X figurasse nell’uno ed X’ nell’altro le due proposizioni si scriverebbero
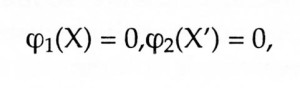
ed in generale non sarebbero più contraddittorie.
Perché dunque i Pragmatisti sollevano quest’obiezione? Perché il genere G non appare loro che come una collezione suscettibile di accrescimento indefinito, man mano che saranno costruiti nuovi individui che possiedono i caratteri giusti; è così che G non può mai essere posto ne varietur, come fanno i Cantoriani, e che non si è sicuri che, per mezzo di nuove annessioni, non diventerà G’.
Mi sono sforzato di spiegare quanto più chiaramente ed imparzialmente possibile in cosa consistano le divergenze tra le due scuole di matematici; e mi sembra che se ne possa già scorgere la causa effettiva; gli studiosi delle due scuole hanno delle attitudini mentali opposte; quelli che ho chiamato Pragmatisti sono idealisti, i Cantoriani sono realisti.
C’è una cosa che ci confermerà in questo modo di vedere. Vediamo che i Cantoriani (che mi si passi questo vocabolo comodo, sebbene non voglia parlare qui dei matematici che seguono la via aperta da Cantor, e forse neanche dei filosofi che a lui si rifanno, ma di quelli che hanno le stesse attitudini in una maniera indipendente), che i Cantoriani, dicevo, parlano costantemente di epistemologia, cioè della scienza delle scienze; ed è ben inteso che tale epistemologia è del tutto indipendente dalla psicologia; essa ci deve cioè insegnare che cosa sarebbero le scienze se non ci fossero scienziati; che dobbiamo studiare le scienze, probabilmente non supponendo che non ci siano scienziati, ma per lo meno senza supporre che ce ne siano. Così, non solo la natura è una realtà indipendente dal fisico che potrebbe essere tentato di studiarla, ma la fisica stessa è inoltre una realtà che sussisterebbe se non ci fossero fisici. Si tratta proprio di realismo.
E perché i Pragmatisti si rifiutano di ammettere oggetti che non potrebbero essere definiti in un numero finito di parole? Perché essi considerano che un oggetto esiste solo quando viene pensato, e che non sapremmo concepire un oggetto pensato indipendentemente da un soggetto pensante. Si tratta proprio di idealismo. E dato che un soggetto pensante è un uomo o qualcosa che assomiglia ad un uomo, e di conseguenza un essere finito, l’infinito non può avere altro senso che la possibilità di creare tanti oggetti finiti quanti vogliamo.
Possiamo allora fare un’osservazione piuttosto curiosa. I realisti si collocano di solito da un punto di vista fisico; sono gli oggetti matematici, o le anime individuali, o ciò che essi chiamano le sostanze, ciò di cui affermano l’esistenza indipendente. Il mondo esisteva per loro prima della creazione dell’uomo, prima ancora di quella degli esseri viventi; ed esisterebbe anche se non ci fosse alcun Dio né alcun soggetto pensante. Questo è il punto di vista del senso comune, ed è solo con la riflessione che si potrà essere indotti ad abbandonarlo. I partigiani del realismo fisico sono in generale finitisti; riguardo al problema delle antinomie kantiane stanno dalla parte della tesi; credono che il mondo sia limitato. Questa è ad esempio la posizione di Evellin. Al contrario gli idealisti non hanno le stesse remore e sono pronti a sottoscrivere le antitesi.
Ma i Cantoriani sono realisti anche per quanto riguarda le entità matematiche; queste entità sembrano loro avere un’esistenza indipendente; il geometra non le crea, le scopre. Questi oggetti esistono quindi, per così dire, senza esistere, dato che si riducono a pure essenze; ma dato che, per natura, questi oggetti sono in numero infinito, i partigiani del realismo matematico sono molto più infinitisti degli idealisti; il loro infinito non è più un divenire, poiché preesiste alla mente che lo scopre; che lo ammettano o che lo neghino, sono dunque costretti a credere nell’infinito attuale.
Riconosciamo la teoria delle idee di Platone; e può sembrare strano vedere Platone classificato tra i realisti; niente è però più antitetico all’idealismo contemporaneo del platonismo, sebbene questa dottrina sia parimenti molto lontana dal realismo fisico. Non ho mai conosciuto un matematico più realista, in senso platonico, di Hermite, e tuttavia devo confessare di non avere mai incontrato nessuno più refrattario al Cantorismo. Si tratta di una contraddizione apparente, tanto più che egli ripeteva volentieri: Sono anticantoriano perché sono realista. Egli rimproverava a Cantor di creare oggetti invece di accontentarsi di scoprirli. Probabilmente a causa delle sue convinzioni religiose considerava come una sorta di empietà voler penetrare direttamente in un dominio che Dio solo poteva abbracciare, senza aspettare che Egli ci rivelasse i misteri uno ad uno. Paragonava le scienze matematiche alle scienze naturali. Un naturalista che avesse tentato di indovinare il segreto di Dio invece di consultare l’esperienza gli sarebbe parso non solo presuntuoso ma anche senza rispetto per la maestà divina; i Cantoriani gli parevano voler agire nella stessa maniera in matematica. Ed è per questo che, realista in teoria, era idealista in pratica. C’è una realtà da conoscere ed essa è esterna a noi ed indipendente da noi; ma tutto quello che ne possiamo conoscere dipende da noi, e non è altro che un divenire, una sorta di stratificazione di conquiste successive. Il resto è reale ma eternamente inconoscibile.
Il caso di Hermite è del resto isolato e non mi dilungherò ancora su di esso. In ogni epoca ci sono state in filosofia tendenze opposte, e non pare che queste tendenze siano sul punto di conciliarsi. Ciò è dovuto probabilmente al fatto che esistono animi differenti e che non si può cambiare niente in questi animi. Non c’è quindi alcuna speranza di vedersi stabilire l’accordo tra Pragmatisti e Cantoriani. Gli uomini non si capiscono perché non parlano la stessa lingua e perché ci sono lingue che non si imparano.
E tuttavia in matematica sono soliti capirsi; ma è proprio grazie a quello che ho chiamato le verifiche; esse costituiscono l’ultimo grado di giudizio, e davanti ad esse tutti si inchinano. Ma laddove queste verifiche vengano meno i matematici non si trovano in posizione migliore dei semplici filosofi. Quando si tratta di sapere se un teorema possa avere un senso senza essere verificabile, chi potrà giudicare, dato che per definizione ci si impedisce di verificare? Non ci sarebbe altra risorsa che ridurre il proprio avversario ad una contraddizione. Ma l’esperimento è stato fatto e non ha dato risultati.
Sono state segnalate molte antinomie, ed il disaccordo è perdurato, nessuno ne è uscito convinto; da una contraddizione ci si può sempre togliere d’impaccio con un espediente, voglio dire con un distinguo.
Jules-Henri Poincaré
Questo saggio di Marcello Cini è già stato pubblicato su Koinè, Periodico culturale, Anno X, nn. 1-2, Gennaio-Giugno 2002, pp. 245-253; direttore responsabile Carmine Fiorillo; il volume collettaneo reca il titolo Scienza cultura, filosofia.Titolo originale: Les mathématiques et la logique, capitolo V di Dernières Pensées. Parigi, Flammarion 1913. Traduzione di FABIO ACERBI.
Koiné
Scienza, Cultura, Filosofia
indice – presentazione – autore – sintesi
Problemi tra scienza e cultura
Sintetizzare e interpretare/Darsi dei limiti/Sulla diffidenza per la filosofia/Una confutazione dello scientismo/I problemi della divulgazione/Specializzazione parcellizzante/Una catastrofe culturale?/Uno sguardo sulla cultura/Linee di resistenza/E se fosse colpa del capitalismo?/Conclusioni. Una modesta utopia.
Lucio Russo
Cosa sta accadendo alla scienza?
Premessa/Cos’è la scienza? La scienza esatta/Scienza esatta e tecnologia /Scienze biologiche (e altre scienze empiriche)/Il problema della verità/Divulgazione scientifica e imposture intellettuali/La crisi attuale/Il nuovo ruolo della biologia: le biotecnologie/Complessità /Quale futuro?
Marcello Cini
C’è ancora bisogno della filosofia per capire il mondo?
Introduzione/La svolta nella scienza dal XX al XXI secolo/L’epistemologia delle scienze della materia inerte/Una epistemologia delle scienze del mondo vivente/Il problema corpo/mente/Scienza e valori/Conclusioni.
Alberto Artosi
Lettera a uno scienziato sulla ragione, la razionalità e il razionalismo
Caro Scienziato/Bisogna guardarsi da un’immagine ingenuamente razionalistica della scienza/Anche gli scienziati più aperti sono dei razionalisti (e degli elitisti) ingenui/Bisogna sottrarsi al culto delle argomentazioni “razionali” /Il caso dell’archeoastronomia/ Il razionalismo ingenuo è intollerante/Sulla “cultura di massa”/Commiato.
Massimo Bontempelli
Il pregiudizio antimetafisico della scienza contemporanea
Popper: la teoria come congettura/Hegel e la filosofia della scienza/La teoria della verità come idealità matematica/Gödel: la logica matematica non può giustificare il proprio principio di coerenza/Matematica senza fondamento/Barrow: la base teorica universale della matematica/Hegel: la quantità come “qualità tolta”/Il gran libro della Natura è scritto in caratteri matematici?/Il risultato culturale della rivoluzione scientifica/La semplificazione galileiana del mondo reale/La quantità matematizzabile come dominabilità del mondo/I limiti del meccanicismo/La fisica delle particelle come pura astrazione teorica/Le teorie del tutto/Il determinismo dell’elettrodinamica quantistica/Feynman: la Natura è assurda/La povertà conoscitiva del determinismo matematico della fisica/Il crollo del determinismo fisico di fronte alle forme biologiche/La concezione biologistica della verità/La povertà della moderna coscienza antimetafisica /Il pregiudizio antimetafisico della mentalità odierna/Realtà e verità nella filosofia ontologic/La sapienza di Platone.
Fabio Bentivoglio
Scienza, Natura e destino dell’uomo. Riflettiamo con Aristotele
Che cosa è, oggi, la sapienza?/La Natura/Le onde e la scogliera/Un’etica per la civiltà tecnologica/Dogmi di ieri e dogmi di oggi/L’elogio del senso comune.
Jean Bricmont
Contro la filosofia della meccanica quantistica
Riassunto/Introduzione/Realismo e positivismo/Il problema della meccanica quantistica/La non località/Soluzioni possibili al problema della misura/Conclusioni/Appendice I: Il problema della misura/Appendice II: Il teorema di Bell/Appendice III: La teoria di Bohm/Appendice IV: Bibliografia/Ringraziamenti/Riferimenti.
Fabio Acerbi
Concetto ed uso dei modelli nella scienza greca antica
Il concetto di modello/La controversia storiografica: strumentalismo versus realismo/Cenni al dibattito epistemologico in età ellenistica/L’approccio per modelli nella scienza antica: alcuni esempi: a. Astronomia; b. Meccanica; c. Ottica; e. Teoria musicale; f. Medicina/Conclusioni.
Jules-Henri Poincaré
La matematica e la logica
***********************************************
Seguici sul sito web
 ***********************************************
***********************************************